In 2012, Andrew Haldane – currently Chief Economist and the Executive Director of Monetary Analysis and Statistics at the Bank of England – delivered a speech to the Federal Reserve Bank of Kansas City’s annual Jackson Hole, Wyoming meeting titled, “The Dog and the Frisbee.” The speech circles the topic of simplicity versus complexity, starting with the simple question: how does a dog know how to catch a frisbee? The mechanics of the process are quite complicated, when we consider the multitude of physical and atmospheric effects that can impact how the frisbee flies. How, then, does a dog achieve this trick without ever learning Newton’s Law of Gravity? As it turns out, the dog can follow a very simple rule (indeed, the very same most humans use): run at a speed such that their gaze at the frisbee remains roughly constant.
As with the dog and the frisbee, when it comes to decision making in inherently uncertain environments, very simple rules and heuristics prove to be incredibly robust in many domains. For example, if you want to predict the winner of Wimbledon, the best model may be simply to ask people outside the stadium which players’ names they recognize. Given that finance, economics, and markets are highly uncertain environments, it would make sense that simple heuristics would prove most effective as well.
Many studies support this conclusion except when simplicity is taken to the extreme. As it turns out, a model that is too simple can prove to be just as fragile as a model that is too complex. Just as a dog does not perform calculus while chasing down a frisbee, it also doesn’t run at a constant speed all the time. The “gaze at a constant angle” model is simple, but still complex enough to be effective.
In the world of tactical investing, the notion of “simple as robust” is often taken to the extreme. We often see investors applying just a single signal to determine large and sudden changes in their portfolios. The problem with such an approach is that the outcome is highly sensitive to small changes in market returns. As an example, consider a model that invests in U.S. equities when the S&P 500 is above its 200-day simple moving average (“200 SMA”) and holds short-term U.S. Treasurys when the S&P 500 falls below its 200 SMA.
Below we plot how far the S&P 500 has been from its 200 SMA over the last several years, with signal changes occurring when the line crosses above or below the 0% threshold. Over this period, we can see two cases where the signal changed due to the S&P 500 falling just below its 200 SMA. We can also see two cases where a signal change was just barely avoided. We can also see a period in Q4 2018 when a cluster of signal changes occurred simultaneously as the S&P 500 danced around its 200 SMA.
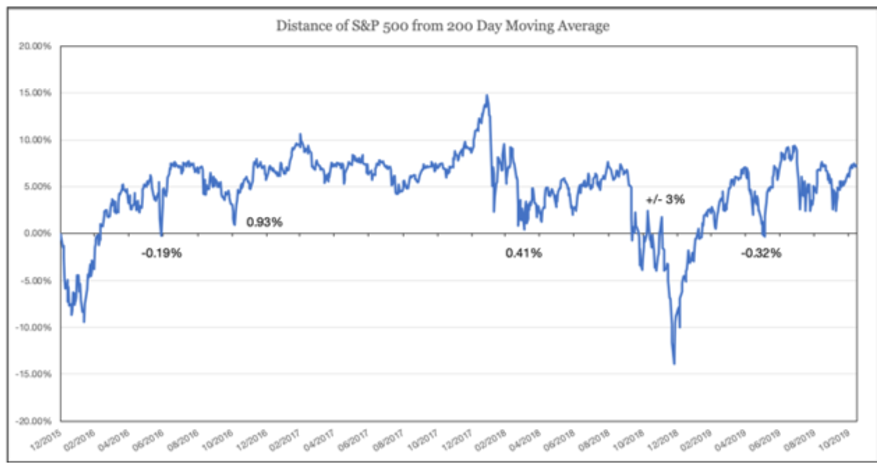
Some answer this fragility problem by adding more complexity to the model; e.g. adding some sort of buffer around the 200 SMA or waiting a certain number of days for confirmation. While this added complexity might address these example issues, they introduce their own corner cases. Others address these problems by sampling their signal less frequently, such as just once a month. This solution introduces an entirely different type of risk: timing luck that occurs due to the approach’s sensitivity to what the signal reads at the time it is reviewed.
In summary, we believe the more appropriate answer to this problem is the same answer investors have used for thousands of years: diversification. Specifically, instead of just using one simple signal to drive our tactical process, we combine a larger number of simple signals. This is akin to saying, “we believe in equities for the long run, but do not want to buy just one stock.” Perhaps more to the point, we believe in the efficacy of many of these tactical signals, but do not to rely on just one approach.

